Skip to main content

11


Access Answers of NCERT Class 9 Maths Chapter 11 – Constructions


Class 9 Maths Chapter 11 Exercise 11.1 Page: 191

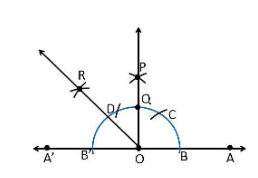
1. Construct an angle of 90° at the initial point of a given ray and justify the construction.
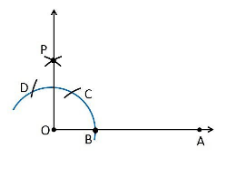
Construction Procedure:
To construct an angle 90°, follow the given steps:
  1. Draw a ray OA
  2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B.
  3. With B as a centre with the same radius, mark a point C on the arc DCB.
  4. With C as a centre and the same radius, mark a point D on the arc DCB.
  5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P.
  6. Finally, the ray OP is joined which makes an angle 90° with OP is formed.
ncert solutions for class 9 maths chapter 11 fig 1
Justification
To prove ∠POA = 90°
In order to prove this draw a dotted line from the point O to C and O to D and the angles formed are:
ncert solutions for class 9 maths chapter 11 fig 2
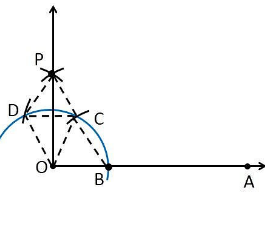
From the construction, it is observed that
OB= BC = OC
Therefore OBC is an equilateral triangle
So that, ∠BOC = 60°.
Similarly,
OD= DC = OC
Therefore DOC is an equilateral triangle
So that, ∠DOC = 60°.
From SSS triangle congruence rule
△OBC ≅ OCD
∠BOC= ∠DOC
Therefore, ∠COP = ½ ∠DOC = ½ (60°).
∠COP = 30°
To find the ∠POA = 90°:
∠POA =∠BOC+ ∠COP
∠POA = 60° +30°
∠POA =90°
Hence, justified.
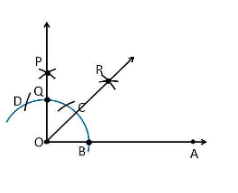
2. Construct an angle of 45° at the initial point of a given ray and justify the construction.
Construction Procedure:
  1. Draw a ray OA
  2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B.
  3. With B as a centre with the same radius, mark a point C on the arc DCB.
  4. With C as a centre and the same radius, mark a point D on the arc DCB.
  5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P.
  6. Finally, the ray OP is joined which makes an angle 90° with OP is formed.
  7. Take B and Q as centre draw the perpendicular bisector which intersects at the point R
  8. Draw a line that joins the point O and R
  9. So, the angle formed ∠ROA = 45°
ncert solutions for class 9 maths chapter 11 fig 3
Justification
From the construction,
∠POA = 90°
From the perpendicular bisector from the point B and Q, which divides the ∠POA into two halves. So it becomes
∠ROA = 1/2 ∠POA
∠ROA = 1/2×90° = 45°
Hence, justified
3. Construct the angles of the following measurements:
(i) 30° (ii) 22 1/2° (iii) 15°
Solution:
(i) 30°
Construction Procedure:
  1. Draw a ray OA
  2. Take O as a centre with any radius, draw an arc BC which cuts OA at B.
  3. With B and C as centres, draw two arcs which intersect each other at the point E and the perpendicular bisector is drawn.
  4. Thus, ∠EOA is the required angle making 30° with OA.
ncert solutions for class 9 maths chapter 11 fig 4
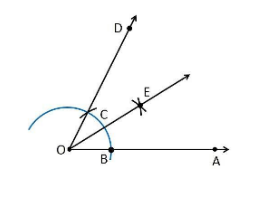
(ii) 22 1/2°
Construction Procedure:
  1. Draw an angle ∠POA = 90°
  2. Take O as a centre with any radius, draw an arc BC which cuts OA at B and OP at Q
  3. Now, draw the bisector from the point B and Q where it intersect at the point R such that it makes an angle ∠ROA = 45°.
  4. Again, ∠ROA is bisected such that ∠TOA is formed which makes an angle of 22.5° with OA
ncert solutions for class 9 maths chapter 11 fig 5
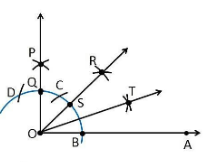
(iii) 15°
Construction Procedure:
  1. An angle ∠DOA = 60° is drawn.
  2. Take O as centre with any radius, draw an arc BC which cuts OA at B and OD at C
  3. Now, draw the bisector from the point B and C where it intersect at the point E such that it makes an angle ∠EOA = 30°.
  4. Again, ∠EOA is bisected such that ∠FOA is formed which makes an angle of 15° with OA.
  5. Thus, ∠FOA is the required angle making 15° with OA.
ncert solutions for class 9 maths chapter 11 fig 6
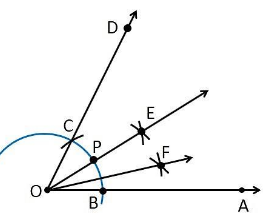
4. Construct the following angles and verify by measuring them by a protractor:
(i) 75° (ii) 105° (iii) 135°
Solution:
(i) 75°
Construction Procedure:
  1. A ray OA is drawn.
  2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA.
  3. With B as centre draw an arc C and C as centre draw an arc D.
  4. With D and C as centre draw an arc, that intersect at the point P.
  5. Join the points O and P
  6. The point that arc intersect the ray OP is taken as Q.
  7. With Q and C as centre draw an arc, that intersect at the point R.
  8. Join the points O and R
  9. Thus, ∠AOE is the required angle making 75° with OA.
ncert solutions for class 9 maths chapter 11 fig 7
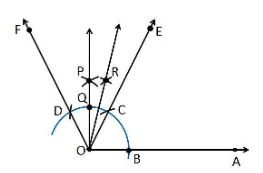
(ii) 105°
Construction Procedure:
  1. A ray OA is drawn.
  2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA.
  3. With B as centre draw an arc C and C as centre draw an arc D.
  4. With D and C as centre draw an arc, that intersect at the point P.
  5. Join the points O and P
  6. The point that arc intersect the ray OP is taken as Q.
  7. With Q and Q as centre draw an arc, that intersect at the point R.
  8. Join the points O and R
  9. Thus, ∠AOR is the required angle making 105° with OA.
ncert solutions for class 9 maths chapter 11 fig 8
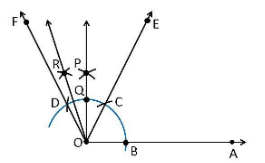
(iii) 135°
Construction Procedure:
  1. Draw a line AOA‘
  2. Draw an arc of any radius that cuts the line AOA‘ at the point B and B‘
  3. With B as centre, draw an arc of same radius at the point C.
  4. With C as centre, draw an arc of same radius at the point D
  5. With D and C as centre, draw an arc that intersect at the point O
  6. Join OP
  7. The point that arc intersect the ray OP is taken as Q and it forms an angle 90°
  8. With B‘ and Q as centre, draw an arc that intersects at the point R
  9. Thus, ∠AOR is the required angle making 135° with OA.
ncert solutions for class 9 maths chapter 11 fig 9
5. Construct an equilateral triangle, given its side and justify the construction.
Construction Procedure:
  1. Let draw a line segment AB=4 cm .
  2. With A and B as centres, draw two arcs on the line segment AB and note the point as D and E.
  3. With D and E as centres, draw the arcs that cuts the previous arc respectively that forms an angle of 60° each.
  4. Now, draw the lines from A and B that are extended to meet each other at the point C.
  5. Therefore, ABC is the required triangle.
ncert solutions for class 9 maths chapter 11 fig 10
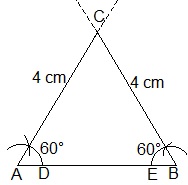
Justification:
From construction, it is observed that
AB = 4 cm, ∠A = 60° and ∠B = 60°
We know that, the sum of the interior angles of a triangle is equal to 180°
∠A + ∠B + ∠C = 180°
SuBstitute the values
⇒ 60° + 60° + ∠C = 180°
⇒ 120° + ∠C = 180°
⇒ ∠C = 60°
While measuring the sides, we get
BC = CA = 4 cm (Sides opposite to equal angles are equal)
AB = BC = CA = 4 cm
∠A = ∠B = ∠C = 60°
Hence, justified.

Class 9 Maths Chapter 11 Exercise 11.2 Page: 195

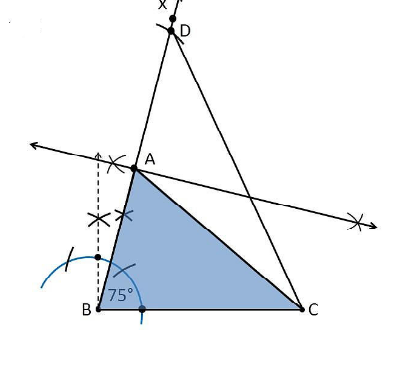
1. Construct a triangle ABC in which BC = 7cm, ∠B = 75° and AB + AC = 13 cm.
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
  1. Draw a line segment of base BC = 7 cm
  2. Measure and draw ∠B = 75° and draw the ray BX
  3. Take a compass and measure AB + AC = 13 cm.
  4. With B as centre and draw an arc at the point be D
  5. Join DC
  6. Now draw the perpendicular bisector of the line BD and the intersection point is taken as A.
  7. Now join AC
  8. Therefore, ABC is the required triangle.
ncert solutions for class 9 maths chapter 11 fig 11
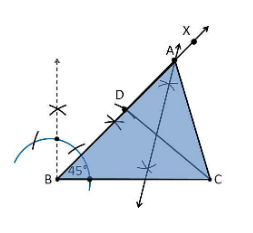
2. Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB – AC = 3.5 cm.
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
  1. Draw a line segment of base BC = 8 cm
  2. Measure and draw ∠B = 45° and draw the ray BX
  3. Take a compass and measure AB – AC = 3.5 cm.
  4. With B as centre and draw an arc at the point be D on the ray BX
  5. Join DC
  6. Now draw the perpendicular bisector of the line CD and the intersection point is taken as A.
  7. Now join AC
  8. Therefore, ABC is the required triangle.
ncert solutions for class 9 maths chapter 11 fig 12
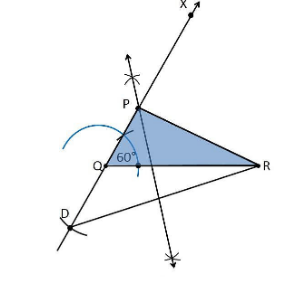
3. Construct a triangle PQR in which QR = 6cm, ∠Q = 60° and PR – PQ = 2cm.
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
  1. Draw a line segment of base QR = 6 cm
  2. Measure and draw ∠Q = 60° and let the ray be QX
  3. Take a compass and measure PR – PQ = 2cm.
  4. Since PR – PQ is negative, QD will below the line QR.
  5. With Q as centre and draw an arc at the point be D on the ray QX
  6. Join DR
  7. Now draw the perpendicular bisector of the line DR and the intersection point is taken as P.
  8. Now join PR
  9. Therefore, PQR is the required triangle.
ncert solutions for class 9 maths chapter 11 fig 13
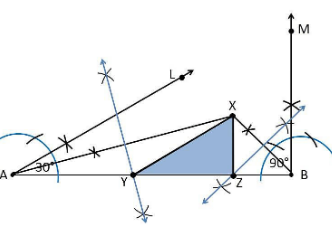
4. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
  1. Draw a line segment AB which is equal to XY + YZ + ZX = 11 cm.
  2. Make an angle ∠Y = 30° from the point A and the angle be ∠LAB
  3. Make an angle ∠Z = 90° from the point B and the angle be ∠MAB
  4. Bisect ∠LAB and ∠MAB at the point X.
  5. Now take the perpendicular bisector of the line XA and XB and the intersection point be Y and Z respectively.
  6. Join XY and XZ
  7. Therefore, XYZ is the required triangle
ncert solutions for class 9 maths chapter 11 fig 14
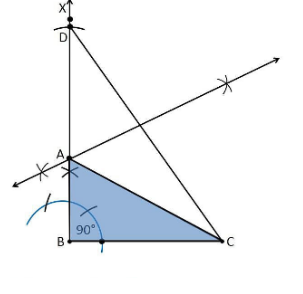
5. Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
  1. Draw a line segment of base BC = 12 cm
  2. Measure and draw ∠B = 90° and draw the ray BX
  3. Take a compass and measure AB + AC = 18 cm.
  4. With B as centre and draw an arc at the point be D on the ray BX
  5. Join DC
  6. Now draw the perpendicular bisector of the line CD and the intersection point is taken as A.
  7. Now join AC
  8. Therefore, ABC is the required triangle.
ncert solutions for class 9 maths chapter 11 fig 15

Comments

Post a Comment

Popular posts from this blog

10

Access Answers of Maths NCERT Class 9 Chapter 10- Circles NCERT Class 9 Maths Solutions For Chapter 10- Circles Class 9 Maths Chapter 10 Exercise: 10.1 (Page No: 171) 1. Fill in the blanks: (i) The centre of a circle lies in ____________ of the circle. (exterior/ interior) (ii) A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior) (iii) The longest chord of a circle is a _____________ of the circle. (iv) An arc is a ___________ when its ends are the ends of a diameter. (v) Segment of a circle is the region between an arc and _____________ of the circle. (vi) A circle divides the plane, on which it lies, in _____________ parts. Solution: (i) The centre of a circle lies in  interior  of the circle. (ii) A point, whose distance from the centre of a circle is greater than its radius lies in  exterior  of the circle. (iii) The longest chord of a circle is...
Post a Comment
Read more

9

Access Answers of Maths NCERT Class 9 Chapter 9 – Areas of Parallelograms and Triangles Class 9 Maths Chapter 9 Exercise 9.1 Page: 155 1. Which of the following figures lie on the same base and in-between the same parallels. In such a case, write the common base and the two parallels. Solution: Trapezium ABCD and ΔPDC lie on the same DC and in-between the same parallel lines AB and DC. Parallelogram PQRS and trapezium SMNR lie on the same base SR but not in-between the same parallel lines. Parallelogram PQRS and ΔRTQ lie on the same base QR and in-between the same parallel lines QR and PS. Parallelogram ABCD and ΔPQR do not lie on the same base but in-between the same parallel lines BC and AD. Quadrilateral ABQD and trapezium APCD lie on the same base AD and in-between the same parallel lines AD and BQ. Parallelogram PQRS and parallelogram ABCD do not lie on the same base SR but in-between the same parallel lines SR and PQ. Exercise 9.2 Page: 159 1. In Fig...
Post a Comment
Read more