3

Access Answers of Maths NCERT class 9 Chapter 3 – Coordinate Geometry

Class 9 Maths Chapter 3 Exercise 3.1 Page: 53

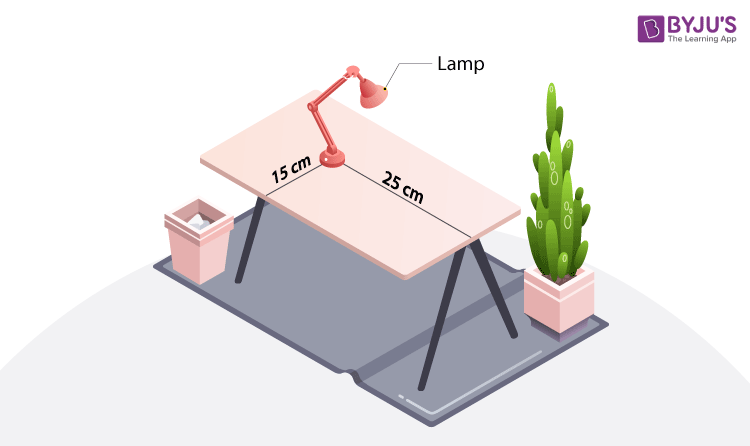
1. How will you describe the position of a table lamp on your study table to another person?
Solution:

For describing the position of table lamp on the study table, we take two lines, a perpendicular and a horizontal line. Considering the table as a plane(x and y axis) and taking perpendicular line as Y axis and horizontal as X axis respectively. Take one corner of table as origin where both X and Y axes intersect each other. Now, the length of table is Y axis and breadth is X axis. From The origin, join the line to the table lamp and mark a point. The distances of the point from both X and Y axes should be calculated and then should be written in terms of coordinates.

The distance of the point from X-axis and Y- axis is x and y respectively, so the table lamp will be in (x, y) coordinate.

Here, (x,y) = (15, 25)

2. (Street Plan) : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.

There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North – South direction and another in the East – West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North – South direction and 5th in the East – West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:

(i) how many cross – streets can be referred to as (4, 3).
(ii) how many cross – streets can be referred to as (3, 4).

Solution:

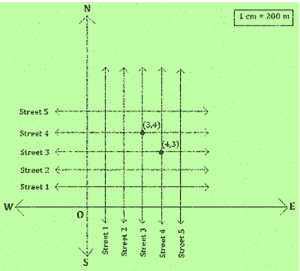(i) Only one street can be referred to as (4,3) (as clear from the figure).
(ii) Only one street can be referred to as (3,4) (as we see from the figure).

Exercise 3.2 Page: 60

1. Write the answer of each of the following questions:

(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.

Solution:

1. The name of horizontal and vertical lines drawn to determine the position of any point in the Cartesian plane is x-axis and y-axis respectively.
2. The name of each part of the plane formed by these two lines x-axis and the y-axis is quadrants.
3. The point where these two lines intersect is called the origin.

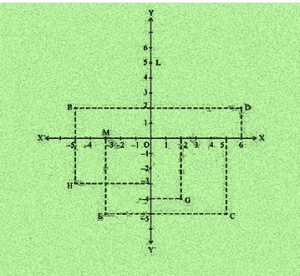
2. See Fig.3.14, and write the following:

1. The coordinates of B.
2. The coordinates of C.
3. The point identified by the coordinates (–3, –5).
4. The point identified by the coordinates (2, – 4).
5. The abscissa of the point D.
6. The ordinate of the point H.
7. The coordinates of the point L.
8. The coordinates of the point M.

Solution:

1. The co-ordinates of B is (−5, 2).
2. The co-ordinates of C is (5, −5).
3. The point identified by the coordinates (−3, −5) is E.
4. The point identified by the coordinates (2, −4) is G.
5. Abscissa means x co-ordinate of point D. So, abscissa of the point D is 6.
6. Ordinate means y coordinate of point H. So, ordinate of point H is -3.
7. The co-ordinates of the point L is (0, 5).
8. The co-ordinates of the point M is (−3, 0).

Exercise 3.3 Page: 65

1. In which quadrant or on which axis do each of the points (– 2, 4), (3, – 1), (– 1, 0),(1, 2) and (– 3, – 5) lie? Verify your answer by locating them on the Cartesian plane.

Solution:

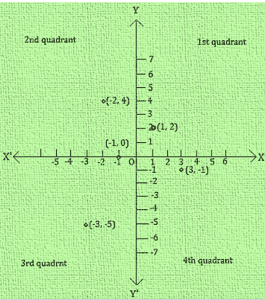
• (– 2, 4): Second Quadrant (II- Quadrant)
• (3, – 1): Fourth Quadrant (IV- Quadrant)
• (– 1, 0): Negative x-axis
• (1, 2): First Quadrant (I- Quadrant)
• (– 3, – 5): Third Quadrant(III- Quadrant)

2. Plot the points (x, y) given in the following table on the plane, choosing suitable units of distance on the axes.

x	-2	-1	0	1	3
y	8	7	-1.25	3	-1

Solution:

The points to plotted on the(x,y) are:

• (-2,8)
• (-1,7)
• (0,-1.25)
• (1,3)
• (3,-1)

On the graph mark X-axis and Y-axis. Mark the meeting point as O.

Now, Let 1 unit = 1 cm

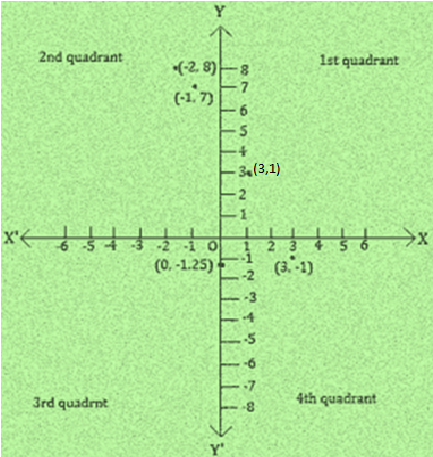
• (-2,8): II- Quadrant, Meeting point of the imaginary lines that starts from 2 units to the left of origin O and from 8 units above the origin O
• (-1,7): II- Quadrant, Meeting point of the imaginary lines that starts from 1 units to the left of origin O and from 7 units above the origin O
• (0,-1.25): On the x-axis, 1.25 units to the left of origin O
• (1,3): I- Quadrant, Meeting point of the imaginary lines that starts from 1 units to the right of origin O and from 3 units above the origin O
• (3,-1): IV- Quadrant, Meeting point of the imaginary lines that starts from 3 units to the right of origin O and from 1 unit below the origin O